Ever wondered why some of your split test results don't quite add up? Or maybe you've rolled out a change that didn't deliver the expected boost? Chances are, Type 1 errors might be playing tricks on your data.
Understanding and reducing these errors isn't just a stats exercise—it's about making smarter decisions that actually move the needle. Let's dive into what Type 1 errors are and how you can minimize them in your split testing.
Understanding the impact of Type 1 errors in split testing
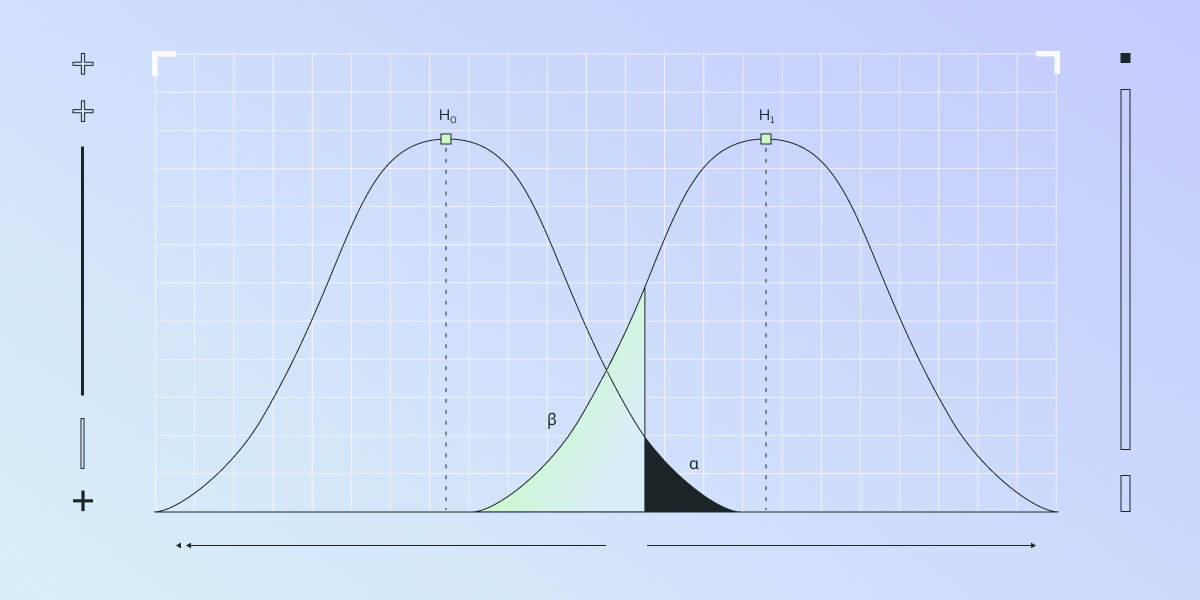
Type 1 errors—also known as false positives—can really throw a wrench in your split testing. Imagine thinking a change made a difference when it actually didn't. It's like chasing shadows. Businesses might pour time and money into adjustments that don't actually improve anything. Wasted resources and misguided decisions are the last things any of us want.
This is why cutting down on Type 1 errors is so crucial. When we reduce false positives, we can trust our test results more and make data-driven decisions that genuinely enhance performance.
Statistical significance is a big player here. A low p-value (typically below 0.05) suggests strong evidence against the null hypothesis, indicating there's a real difference between your test variations. But be careful—set your significance levels wisely to balance the risk of Type 1 and Type 2 errors.
There are a few strategies you can use: optimizing sample size, applying sequential testing, or diving into Bayesian statistics. Tools like Statsig's sample size calculator can help you figure out the optimal sample size for your tests.
By getting a handle on Type 1 errors and taking steps to minimize them, you'll ensure your split testing delivers reliable, actionable insights. This empowers you to make informed decisions that really boost your product or service. At Statsig, we're all about helping you make those smart moves.
Statistical strategies to minimize Type 1 errors
Optimizing your sample size is key to cutting down Type 1 errors. Bigger sample sizes ramp up your statistical power, making your tests more likely to spot true effects and less likely to produce false positives.
Another approach is balancing your significance levels. Setting a lower significance level (say, 0.01 instead of 0.05) reduces the risk of Type 1 errors but might bump up Type 2 errors. It's all about finding that sweet spot based on what's at stake with each error type. Careful consideration is essential here.
Sequential testing is also worth considering. It involves checking data at set intervals during your experiment. This way, you can stop early if you've gathered enough evidence, cutting down the chance of false positives. Sequential testing shines in online experiments where data comes in continuously.
Don't forget about multiple testing correction methods like the Bonferroni correction. These help control the familywise error rate when you're running multiple comparisons. By adjusting the significance level for each test, you keep the overall Type 1 error rate where you want it, preventing inflation due to multiple testing.
Putting these strategies into action takes some statistical know-how and careful planning. Tools like Statsig make it easier, offering features for sample size calculation, significance level tweaks, and sequential testing.
Advanced methods for reducing Type 1 errors
If you're looking to level up, Bayesian statistics might be your next stop. By incorporating prior knowledge, Bayesian methods weigh your test results against existing evidence, helping you spot and reduce false positives. It's a powerful way to get a more nuanced view of your data. You can learn more about this approach in our blog post.
When you're juggling multiple comparisons, the risk of Type 1 errors climbs. Applying corrections like the Bonferroni adjustment helps keep things in check. These adjustments control the familywise error rate, ensuring your overall Type 1 error rate stays where you need it.
Another smart move is pre-registering your hypotheses. By spelling out your hypotheses, analysis plan, and decision rules before you start, you avoid data dredging and confirmation bias. This keeps false-positive rates from creeping up.
These advanced tactics build on the basics we talked about earlier—like optimizing sample size and balancing significance levels. By mixing and matching these approaches, you can seriously cut down the chance of Type 1 errors. That means more reliable and actionable results from your A/B tests.
Practical tips and tools for effective split testing
First off, ensure your data quality is top-notch. Use validation techniques like cross-validation and handle outliers properly to keep your data clean. Good data means more trustworthy results and better decisions.
Keep an eye on practical significance, not just statistical significance. Sure, a p-value can tell you something's happening, but is it a big enough effect to matter? Assess the effect size and think about the real-world impact. This helps you focus on changes that truly make a difference.
Make the most of platforms like Statsig and Python libraries to boost your testing and analysis. Statsig simplifies the whole process—from setting up your test to crunching the numbers—making data-driven decision-making a breeze. Python libraries like SciPy and Pandas are great for complex data manipulation and analysis, helping you run thorough split tests.
Don't underestimate the power of data visualization. Tools like Matplotlib and Seaborn help you see what's going on in your data. Visuals can reveal patterns or anomalies that might be hidden in spreadsheets. Plus, they're great for sharing your findings with the team.
Finally, always iterate and refine your split testing process. As you gather more data and learn from each test, you'll get better at predicting outcomes and making adjustments. Regularly review your methods, get feedback, and stay updated with best practices. This keeps your split tests effective and reliable.
Closing thoughts
Reducing Type 1 errors in your split testing isn't just about avoiding mistakes—it's about making confident, informed decisions that drive real improvements. By combining statistical strategies with practical tools, you can minimize false positives and trust your results. Remember, at Statsig, we're here to help you navigate these challenges and optimize your testing efforts.
Ready to dive deeper? Check out our resources and tools to take your split testing to the next level. Hope you found this helpful!